Constanta de timp a unei bobine
Constanta de timp a unei bobine
Formula
Formula randată:
Cod LaTeX:
Exemple de utilizare
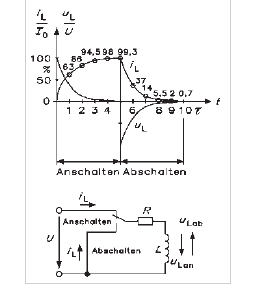
Pornire:
\( \begin{aligned}& i_{\mathrm{L}}=\frac{U}{R} \cdot\left(1-e^{-t / \tau}\right) \\& u_{\mathrm{L}}=U \cdot e^{-t / \tau}\end{aligned} \)
Oprire:
\( \begin{aligned}& i_{\mathrm{L}}=\frac{U}{R} \cdot e^{-t / \tau} \\& u_{\mathrm{L}}=-U \cdot e^{-t / \tau}\end{aligned} \)
τ*-Constanta de timp în s
iL-Valoarea instantanee a curentului în bobină
t-Timpul după începerea sau întreruperea
Exemplu: R = 100 Ω; L = 1 H; U = 10 V; t = 25 ms; iL = ?
\( \tau=\frac{1 \mathrm{H}}{100 \Omega}=10 \mathrm{~ms} ; \quad i_{\mathrm{L}}=\frac{10 \mathrm{~V}}{100 \Omega} \cdot\left(1-e^{-25 \mathrm{~ms} / 10 \mathrm{~ms}}\right)=92 \mathrm{~mA} \)
\( \begin{aligned}& i_{\mathrm{L}}=\frac{U}{R} \cdot\left(1-e^{-t / \tau}\right) \\& u_{\mathrm{L}}=U \cdot e^{-t / \tau}\end{aligned} \)
Oprire:
\( \begin{aligned}& i_{\mathrm{L}}=\frac{U}{R} \cdot e^{-t / \tau} \\& u_{\mathrm{L}}=-U \cdot e^{-t / \tau}\end{aligned} \)
τ*-Constanta de timp în s
iL-Valoarea instantanee a curentului în bobină
t-Timpul după începerea sau întreruperea
Exemplu: R = 100 Ω; L = 1 H; U = 10 V; t = 25 ms; iL = ?
\( \tau=\frac{1 \mathrm{H}}{100 \Omega}=10 \mathrm{~ms} ; \quad i_{\mathrm{L}}=\frac{10 \mathrm{~V}}{100 \Omega} \cdot\left(1-e^{-25 \mathrm{~ms} / 10 \mathrm{~ms}}\right)=92 \mathrm{~mA} \)
Schema electrică
