Generator de tensiune cu sarcina
Descriere
Un generator de tensiune care alimentează un circuit extern, având în vedere atât rezistența internă a generatorului, cât și rezistența de sarcină. Aceasta influențează distribuția tensiunii și curentului în circuit, afectând performanța și eficiența sistemului.
Formula
\( \begin{aligned}
& U=U_{\mathrm{q}}-I \cdot R_{\mathrm{i}} \\
& I=\frac{U_{\mathrm{q}}}{R_{\mathrm{i}}+R_{\mathrm{L}}} ; \quad I_{\mathrm{k}}=\frac{U_{\mathrm{q}}}{R_{\mathrm{i}}} \\
& R_{\mathrm{i}}=\frac{U_{\mathrm{q}}}{I_{\mathrm{k}}}=\left|\frac{\Delta U}{\Delta I}\right|
\end{aligned} \)
Nu ai înțeles ceva? Încearcă cu AI
Science Stories
Explicație
Schema electrică
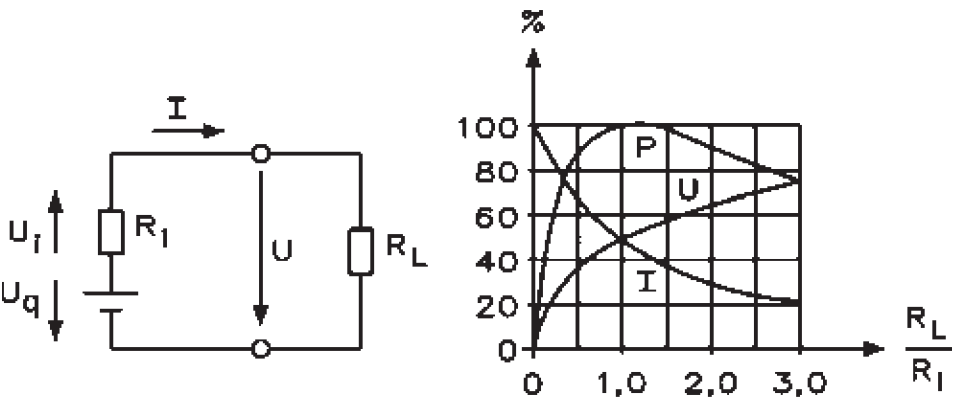
Exemple
U tensiunea la borne
Uq tensiunea sursei, tensiunea în gol
I curent
Ik curent de scurtcircuit
I variația curentului
ΔU variația tensiunii
RL rezistența de sarcină
Ri rezistența internă
Pmax puterea maximă
Când Ri = RL (caz special), atunci se aplică:
\( P_{\max }=\frac{U_q^2}{4 \cdot R_{\mathrm{i}}} ; \quad U=\frac{U_{\mathrm{q}}}{2} ; \quad I=\frac{U_{\mathrm{q}}}{2 \cdot R_{\mathrm{L}}} \)
Ajustarea tensiunii: RL > Ri
Ajustarea puterii: RL = Ri
Ajustarea curentului: RL < Ri
Exemplu: \( U_{\mathrm{q}}=1,5 \mathrm{~V} ; R_{\mathrm{i}}=0,5 \Omega ; R_{\mathrm{L}}=1,5 \Omega ; I=? ; I_{\mathrm{k}}=? ; P_{\max }=\text { ? } \)
\( I=\frac{1,5 \mathrm{~V}}{0,5 \Omega+1,5 \Omega}=0,75 \mathrm{~A} \)
\( I_{\mathrm{k}}=\frac{1,5 \mathrm{~V}}{0,5 \Omega}=3 \mathrm{~A} \)
\( P_{\max }=\frac{(1,5 \mathrm{~V})^2}{4 \cdot 0,5 \Omega}=1,125 \mathrm{~W} \)
Uq tensiunea sursei, tensiunea în gol
I curent
Ik curent de scurtcircuit
I variația curentului
ΔU variația tensiunii
RL rezistența de sarcină
Ri rezistența internă
Pmax puterea maximă
Când Ri = RL (caz special), atunci se aplică:
\( P_{\max }=\frac{U_q^2}{4 \cdot R_{\mathrm{i}}} ; \quad U=\frac{U_{\mathrm{q}}}{2} ; \quad I=\frac{U_{\mathrm{q}}}{2 \cdot R_{\mathrm{L}}} \)
Ajustarea tensiunii: RL > Ri
Ajustarea puterii: RL = Ri
Ajustarea curentului: RL < Ri
Exemplu: \( U_{\mathrm{q}}=1,5 \mathrm{~V} ; R_{\mathrm{i}}=0,5 \Omega ; R_{\mathrm{L}}=1,5 \Omega ; I=? ; I_{\mathrm{k}}=? ; P_{\max }=\text { ? } \)
\( I=\frac{1,5 \mathrm{~V}}{0,5 \Omega+1,5 \Omega}=0,75 \mathrm{~A} \)
\( I_{\mathrm{k}}=\frac{1,5 \mathrm{~V}}{0,5 \Omega}=3 \mathrm{~A} \)
\( P_{\max }=\frac{(1,5 \mathrm{~V})^2}{4 \cdot 0,5 \Omega}=1,125 \mathrm{~W} \)