Legarea în paralel a rezistențelor
Descriere
Într-un circuit paralel, conductanțele (G) se adună direct, iar rezistențele (R) se combină prin inversare. Asta înseamnă că pentru a găsi rezistența totală (R_total), întâi calculăm inversul fiecărei rezistențe individuale, adunăm aceste valori, și apoi luăm inversul sumei obținute.
Formula
\( \begin{aligned}
& \frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\ldots \\
& I=I_1+I_2+I_3+\ldots ; G=G_1+G_2+G_3+\ldots
\end{aligned} \)
Nu ai înțeles ceva? Încearcă cu AI
Science Stories
Explicație
Schema electrică
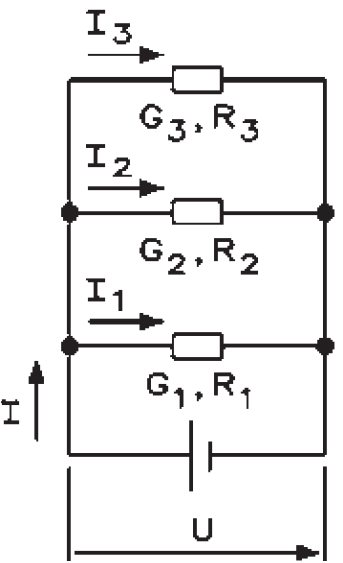
Exemple
I Curentul total în A
I_1, I_2, I_3 Curentul parțial în A
G Conductanța totală în Siemens sau mho
G_1, G_2, G_3 Conductanțele parțiale în Siemens sau mho
R Rezistența totală în Ω
R_1, R_2, R_3 Rezistențele individuale în Ω
1. Caz special: Două rezistențe în paralel:
\( R=\frac{R_1 \cdot R_2}{R_1+R_2} ; \quad R_1=\frac{R_2 \cdot R}{R_2-R} \)
2. Caz special: Rezistențe identice în paralel:
\( R_G = \frac{R_E}{n} \)
n Numărul de rezistențe identice
R_G Rezistența totală
R_E Rezistența individuală
Exemplu: U = 10 V; R_1 = 10 Ω; R_2 = 20 Ω; R = ?; G = ?; I = ?
\( R=\frac{10 \Omega \cdot 20 \Omega}{10 \Omega+20 \Omega}=6,67 \Omega \)
\( G=\frac{1}{R}=\frac{1}{6,67 \Omega}=0,15 \mathrm{~S}\)
\( I=\frac{U}{R}=\frac{10 \mathrm{~V}}{6,67 \Omega}=1,5 \mathrm{~A}\)
I_1, I_2, I_3 Curentul parțial în A
G Conductanța totală în Siemens sau mho
G_1, G_2, G_3 Conductanțele parțiale în Siemens sau mho
R Rezistența totală în Ω
R_1, R_2, R_3 Rezistențele individuale în Ω
1. Caz special: Două rezistențe în paralel:
\( R=\frac{R_1 \cdot R_2}{R_1+R_2} ; \quad R_1=\frac{R_2 \cdot R}{R_2-R} \)
2. Caz special: Rezistențe identice în paralel:
\( R_G = \frac{R_E}{n} \)
n Numărul de rezistențe identice
R_G Rezistența totală
R_E Rezistența individuală
Exemplu: U = 10 V; R_1 = 10 Ω; R_2 = 20 Ω; R = ?; G = ?; I = ?
\( R=\frac{10 \Omega \cdot 20 \Omega}{10 \Omega+20 \Omega}=6,67 \Omega \)
\( G=\frac{1}{R}=\frac{1}{6,67 \Omega}=0,15 \mathrm{~S}\)
\( I=\frac{U}{R}=\frac{10 \mathrm{~V}}{6,67 \Omega}=1,5 \mathrm{~A}\)